2.2.4 Standard Deviation and Turbulence Data
The
standard deviation of the azimuth and elevation angles of the wind vector,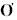 
A and
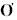E ,
respectively can be related to the dispersive capabilities of the
atmosphere, in particular, to the dispersion coefficients 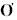y and 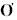z which
characterize plume concentration distributions in commonly-used Gaussian
models. These quantities can be used as inputs to algorithms to determine
Pasquill stability categories (see Section 6.4.4), or may also be treated as
turbulence data for direct input to certain Gaussian models.
The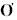
values should be computed directly from high-speed analog or digital
data records (Section 6.1). If a sigma meter or sigma computer is used, care
should be taken that the results are not biased by smoothing of the data,
and to ensure that the methods employed accurately treat the 0-360°
crossover and use an adequate number of samples (at least 360 per
averaging period, see Section 6.1.4). The comparability of results from the
sigma computer to the direct statistical approach should be demonstrated. To
accurately determine 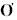A
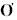and E , the wind
direction sensors must possess certain minimum response characteristics.
The most important in this regard is the damping ratio, which should be
between 0.4 to 0.7 (see Section 5.2). The wind direction should also be
recorded to a resolution of 1 degree in order to calculate the standard
deviation.
2. PRIMARY METEOROLOGICAL VARIABLES
2.1 Wind Speed
2.1.1 Cup Anemometers
2.1.2 Vane-oriented and Fixed-mount Propeller Anemometers
2.1.3 Wind Speed Transducers
2.2 Wind Direction
2.2.1 Wind Vanes
2.2.2 U-V and UVW Systems
2.2.3 Wind Direction Transducers
2.2.4 Standard Deviation and Turbulence
Data
2.3 Temperature and Temperature Difference
2.3.1 Classes of Temperature Sensors
2.3.2 Response Characteristics
2.3.3 Temperature Difference
2.3.4 Sources of Error
2.4 Humidity
2.4.1 Humidity Variables
2.4.2 Types of Instrumentation
2.5 Precipitation
2.6 Pressure
2.7 Radiation
2.8 Recommendations
