6.2.1 Scalar Computations

The scalar mean wind speed is:

The harmonic mean wind speed is:

The standard deviation of the horizontal component of the wind speed is:

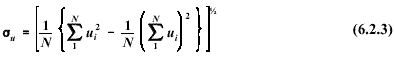
The wind direction is a circular function with values between l and 360 degrees. The wind direction discontinuity at the beginning/end of the scale requires special processing to compute a valid mean value. A single-pass procedure developed by Mitsuta and documented in reference [23] is recommended. The method assumes that the difference between successive wind direction samples is less than 180 degrees; to ensure such, a sampling rate of once per second or greater should be used (see Section 6.2.4). Using the Mitsuta method, the scalar mean wind direction is computed as:

The following notes/cautions apply to the determination of the scalar mean wind direction using Equation. 6.2.4:

• If the result is less than zero or greater than 360, increments of 360 degrees should be added or subtracted, as appropriate, until the result is between zero and 360 degrees.
• Erroneous results may be obtained if this procedure is used to post-process sub-hourly averages to obtain an hourly average. This is because there can be no guarantee that the difference between successive sub-hourly averages will be less than 180 degrees.

The scalar mean wind direction, as defined in Equation. 6.2.4, retains the essential statistical property of a mean value, namely that the deviations from the mean must sum to zero:

By definition, the same mean value must be used in the calculation of the variance of the wind direction and, likewise, the standard deviation (the square root of the variance). The variance of the wind direction is given by:
 

The standard deviation of the wind direction using the Mitsuta method is given by:

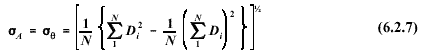
Cases may arise in which the sampling rate is insufficient to assure that differences between successive wind direction samples are less than 180 degrees. In such cases, approximation formulas may be used for computing the standard deviation of the wind direction. Mardia [24] shows that a suitable estimate of the standard deviation (in radian measure) is:

Several methods for calculating the standard deviation of the wind direction were evaluated by Turner [25]; a method developed by Yamartino [26] was found to provide excellent results for most cases. The Yamartino method is given in the following:

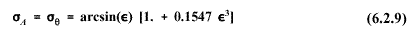
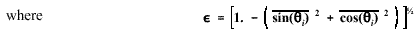
Note that hourly _ _ values computed using 6.2.7, 6.2.8, or 6.2.9 may be inflated by contributions from long period oscillations associated with light wind speed conditions (e.g.,wind meander). To minimize the effects of wind meander, the hourly 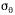(for use e.g., in stability determinations - see Section 6.4.4.4) should be calculated based on four 15-minute values averaged as follows:

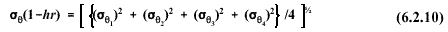
The standard deviation of the vertical component of the wind speed is:

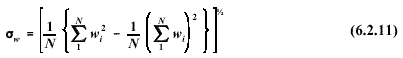
Similarly, the standard deviation of the elevation angle of the wind vector is:
 

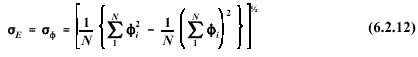
Equation 6.2.12 is provided for completeness only. The bivane, which is used to measure the elevation angle of the wind, is regarded as a research grade instrument and is not recommended for routine monitoring applications. See Section 6.2.3 for recommendations on estimating.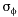

6. METEOROLOGICAL DATA PROCESSING
  6.1 Averaging and Sampling Strategies 
  6.2 Wind Direction and Wind Speed 
      6.2.1 Scalar Computations 
      6.2.2 Vector Computations 
      6.2.3 Treatment of Calms  
      6.2.4 Turbulence 
      6.2.5 Wind Speed Profiles  
  6.3 Temperature 
      6.3.1 Use in Plume-Rise Estimates  
      6.3.2 Vertical Temperature Gradient 
  6.4 Stability 
      6.4.1 Turner's method  
      6.4.2 Solar radiation/delta-T (SRDT) method 
      6.4.3  _E method 
      6.4.4 _Amethod 
      6.4.5 Accuracy of stability category estimates 
  6.5 Mixing Height 
      6.5.1 The Holzworth Method  
  6.6 Boundary Layer Parameters  
      6.6.1 The Profile Method 
      6.6.2 The Energy Budget Method  
      6.6.3 Surface Roughness Length 
      6.6.4 Guidance for Measurements in the Surface Layer 
  6.7 Use of Airport Data 
  6.8 Treatment of Missing Data  
      6.8.1 Substitution Procedures 
  6.9 Recommendations