6.2.2 Vector Computations

From the sequence of N observations of 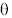_i and u_i, the mean east-west, V_e, and north-south, V_n, components of the wind are:

The resultant mean wind speed and direction are:

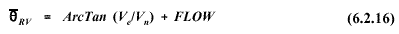
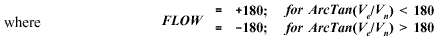
Equation 6.2.16 assumes the angle returned by the ArcTan function is in degrees. This is not always the case and depends on the computer processor. Also, the ArcTan function can be performed several ways. For instance, in FORTRAN either of the following forms could be used:

ATAN ( Ve /Vn )

or ATAN2 (Ve , Vn ).

The ATAN2 form avoids the extra checks needed to insure that V_n is nonzero, and is defined over a full 360 degree range.

The unit vector approach to computing mean wind direction is similar to the vector mean described above except that the east-west and north-south components are not weighted by the wind speed. Using the unit vector approach, equations 6.2.13 and 6.2.14 become

The unit vector mean wind direction is:

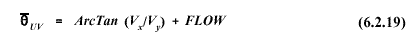
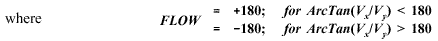
In general, the unit vector result will be comparable to the scalar average wind direction, and may be used to model plume transport.

6. METEOROLOGICAL DATA PROCESSING
  6.1 Averaging and Sampling Strategies 
  6.2 Wind Direction and Wind Speed 
      6.2.1 Scalar Computations 
      6.2.2 Vector Computations 
      6.2.3 Treatment of Calms  
      6.2.4 Turbulence 
      6.2.5 Wind Speed Profiles  
  6.3 Temperature 
      6.3.1 Use in Plume-Rise Estimates  
      6.3.2 Vertical Temperature Gradient 
  6.4 Stability 
      6.4.1 Turner's method  
      6.4.2 Solar radiation/delta-T (SRDT) method 
      6.4.3  _E method 
      6.4.4 _Amethod 
      6.4.5 Accuracy of stability category estimates 
  6.5 Mixing Height 
      6.5.1 The Holzworth Method  
  6.6 Boundary Layer Parameters  
      6.6.1 The Profile Method 
      6.6.2 The Energy Budget Method  
      6.6.3 Surface Roughness Length 
      6.6.4 Guidance for Measurements in the Surface Layer 
  6.7 Use of Airport Data 
  6.8 Treatment of Missing Data  
      6.8.1 Substitution Procedures 
  6.9 Recommendations